Diagramma a scala logaritimica
Alcuni suggerimenti per ottimizzare i grafici.
Spesso utilizziamo i grafici per la loro proprietà di rendere immediatamente comprensibile un fenomeno che abbiamo analizzato.
Comunemente denotiamo infatti con l'espressione "grafici parlanti" quelli che hanno una grande capacità esplicativa.
Tuttavia, è necessario sapersi districare all'interno della vasta tipologia di grafici disponibili poiché, soltanto adottando quello giusto, la nostra serie verrà correttamente rappresentata. Infatti, la lettura degli schemi conclusivi è suscettibile di un elevato grado di soggettività, con il duplice rischio di porre in evidenza ciò che è banale e di tralasciare ciò che é davvero importante, talora essenziale.
Vediamo quindi insieme come scegliere il grafico che abbia il più alto potere esplicativo.
Occorre innanzitutto distinguere i tipi di serie (caratteri qualitativi) e di seriazione
(caratteri quantitativi) a cui appartengono i nostri dati,
poiché a ciascuno di essi si associa al meglio un solo tipo di grafico.
- Sconnesse (es.: personale occupato presso i servizi bancari).
- Rettilinee (es.: i gradi gerarchici).
- Cicliche (es.: le stagioni).
- Temporali.
1) Continue (es.: l'andamento di alcuni titoli azionari).
2) Semicontinue (es.: tempi d'utilizzo del parco macchine).
3) Discontinue (es.: la produzione di grano).
Concluderemo con una rassegna di alcuni suggerimenti per ottimizzare i grafici.
Alle serie vanno associati i diagrammi a rettangoli 1, circolari, areali e gli ideogrammi. Alle serie temporali si associano i diagrammi a segmenti, a linea curva e linea spezzata. Alle seriazioni vanno associati i diagrammi ad aste (nel caso discreto) e i diagrammi a rettangolo e a canna d'organo 2 (nel caso continuo).
N.B.: nelle seriazioni di tipo continuo le modalità di osservazione sono definite in classi di intervallo, le quali devono essere costruite in modo che:
· gli intervalli siano disgiunti, non abbiano cioè punti in comune;
· le classi non siano vuote né troppo numerose.
Calcolare l'ampiezza delle classi nel modo seguente:
Ac = (VALOREmax - VALOREmin / (1 + 3,32logN) |
Esempio:
|
Dattilografe |
Produzione di fogli al giorno |
| A | 73 |
| B | 109 |
| C | 119 |
| D | 125 |
| E | 93 |
| F | 227 |
| G | 133 |
| H | 122 |
| I | 115 |
Problema:
per studiare il fenomeno dobbiamo raggruppare in classi la produzione giornaliera di fogli.
Ac = 40 (circa). Quindi avremo: |
Produzione (X) |
Numero di dattilografe (Frequenze) | |
70 --I 110 |
3 | |
110 --I 150 |
5 | |
150 --I 190 |
0 | |
190 --I 230 |
1 | |
9 | ||
Le serie sconnesse, rettilinee e cicliche : diagrammi a rettangoli, circolari e areali, ideogrammi.
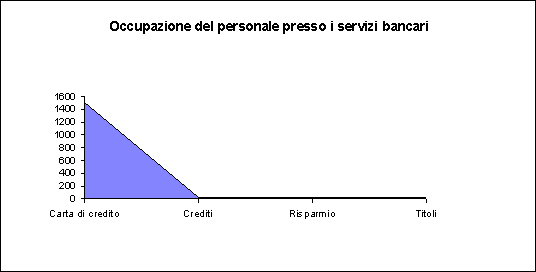
Esempio: Personale occupato presso i servizi bancari.
Servizi bancari (X) |
Personale occupato (f) |
Carte di credito |
1500 |
Crediti |
30 |
Risparmio |
20 |
Titoli |
28 |
1578 |
Si tratta quindi di una serie sconnessa (1500 è, infatti è un valore molto grande in relazione agli altri valori della serie)
Ricorrendo all'Excel3 otteniamo, quindi, il seguente grafico di difficile lettura:
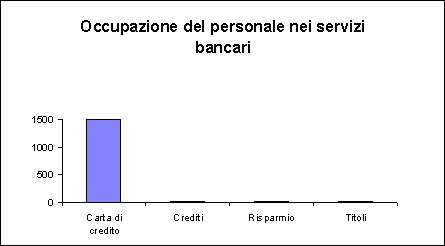
Vero è che se il valore massimo fosse stato anziché 1500, 150 lo stesso grafico risulterebbe leggibile. Infatti si avrebbe:
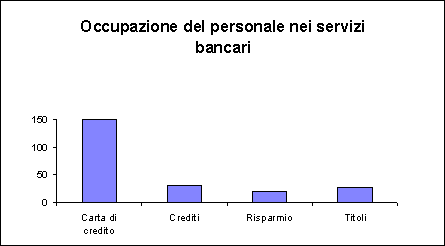
Pertanto, essendo la serie sconnessa (nel nostro caso la distanza tra il valore massimo e quello subito inferiore è di molto maggiore rispetto a tutte le altre distanze), il grafico da utilizzare è il seguente, purtroppo non disponibile in Excel, in quanto non è possibile spezzare la scala di misura:
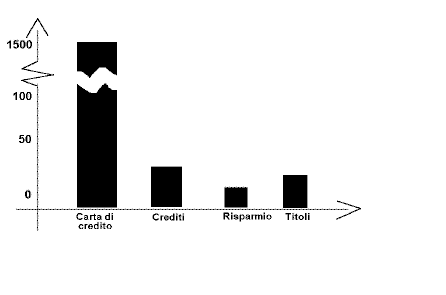
In alternativa, ma con l'evidente perdita dell'informazione che la serie è sconnessa e con un effetto visivo non ottimale, si possono adottare i diagrammi circolari e areali e gli ideogrammi (non disponibili in Excel).
Questi ultimi quindi, hanno un potere esplicativo pari a quello fornito dal
diagramma a rettangoli nel caso la serie sia rettilinea o ciclica (cioè non sconnessa).
Diagramma circolare (sconsigliato per serie sconnesse).
I settori circolari devono avere un'area proporzionale alla quantità da rappresentare:
3600 = intensità (o frequenza) totale.
a = intensità (o frequenza) relativa.
Sicché: 360 / 1578 = 0,2281368
X |
f |
a = 0,2281368 . f | |
Carte di credito |
1500 |
342,20 | |
Crediti |
30 |
6,85 | |
Risparmio |
20 |
4,56 | |
Titoli |
28 |
6,39 | |
360,00 | |||
L'aver calcolato i valori di a ci permette di costruire da soli "con carta e penna" il diagramma circolare (o torta).
In alternativa, utilizzando l'Excel, otteniamo il seguente (e brutto) grafico:
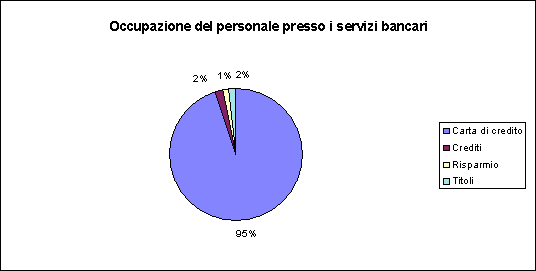
Diagramma areale (sconsigliato per serie sconnesse).
Infatti:
Ideogramma (sconsigliato per serie sconnesse).
Infatti, posto:
![]() = 15
= 15
si avrebbero 100 "omini" per la voce "carte di credito",
2 "omini" per la voce "crediti",
1 "omino" senza una gamba né un braccio per la voce Risparmio
ed 1 "omino" senza un braccio per la voce Titoli !
Le serie temporali continue, semicontinue e discontinue: istogrammi, curve e spezzate.
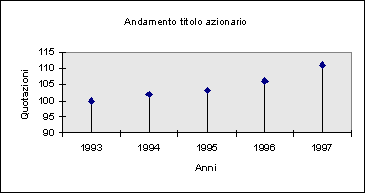
Esempio: andamento di alcuni titoli azionari (serie temporale continua).
Diagramma ad aste (nel caso di un solo titolo azionario).
Anni: |
1993 |
1994 |
1995 |
1996 |
1997 |
Quotazioni: |
100 |
102 |
103 |
106 |
111 |
Esistono delle rappresentazioni che utilizzano
anziché le frequenze semplici,
le frequenze cumulate.
Esempio: giorni occorrenti ad un plico di lettere per raggiungere l'ufficio destinatario.
Giorni (X) |
Frequenze |
Frequenze cumulate (F) | |
1 |
157 |
157 | |
2 |
419 |
567 | |
3 |
890 |
1457 | |
4 |
215 |
1672 | |
5 |
120 |
1792 | |
6 |
150 |
1942 | |
7 |
95 |
2037 | |
2037 |
|||
Questo tipo di grafico, non disponibile in Excel, è l'unico ad illustrare il quantitativo di lettere pervenute a destinazione nell'arco del giorno.
Inoltre è indispensabile utilizzare le frequenze cumulate per rendersi conto in un tal giorno quante lettere sono pervenute sino a quel momento.
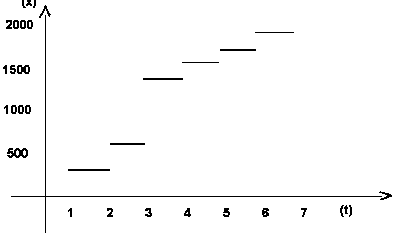
Diagramma a canne d'organo (alcuni titoli azionari).
Sia la seguente tabella a doppia entrata:
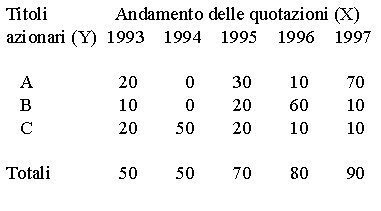
La sua rappresentazione grafica è la seguente:
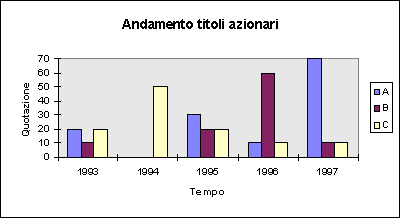
I rettangoli (le canne d'organo) rappresentano le aste e vengono usate per comodità (per distinguerle tra loro all'interno del medesimo raggruppamento).
Esempio: tempi di utilizzazione (minuti al giorno) del parco macchine (serie temporale semicontinua).
Minuti |
f |
Frequenze cumulate (F) | |
50 --I 100 |
5 |
5 | |
100 --I 150 |
6 | 11 | |
150 --I 200 |
15 |
26 | |
200 --I 250 |
20 |
46 | |
250 --I 300 |
12 |
58 | |
300 --I 350 |
2 |
60 | |
60 |
|||
Il grafico da utilizzare per serie di questo tipo è il seguente.
Si noti come anche in questo caso è opportuno utilizzare le frequenze cumulate per una visualizzazione che sia la più esplicativa possibile.
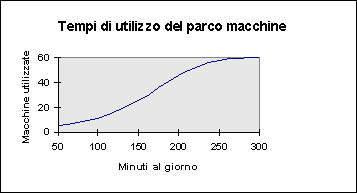
Diagramma a scala logaritmica.
Esempio: la produzione di grano (serie temporale discontinua).
Sia:
Annate (X) |
Quintali (f) |
1 |
35 |
2 |
25 |
3 |
20 |
4 |
40 |
5 |
10 |
6 |
5 |
Si potrebbe semplicemente rappresentare l'andamento della produzione di grano lungo il tempo, adottando pertanto il seguente grafico:
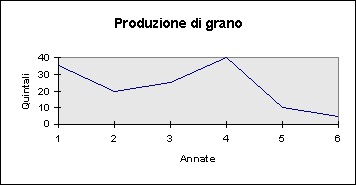
Tuttavia, qualora fossimo interessati, come è plausibile, a dare risalto alla variazione di ogni intensità o frequenza rispetto alle altre, utilizzeremo la scala logaritmica.
Il grafico risultante è pertanto il seguente:
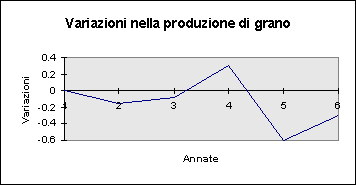
dove ogni punto sul grafico è un rapporto.
Ad esempio, nonostante l'annata 3 abbia segnato un calo di produzione rispetto all'annata precedente, l'andamento è positivo poiché la perdita è stata inferiore a quella verificatasi l'annata 2 rispetto all'annata 1!
Le seriazioni: caso discreto (diagrammi ad asta) e caso continuo (istogrammi e poligoni di frequenza).
Esempio: anni di anzianità del personale (caso discreto, diagramma ad aste).
Anzianità (X) |
Collaboratori (f) |
1 |
3 |
2 |
2 |
3 |
2 |
4 |
4 |
5 |
1 |
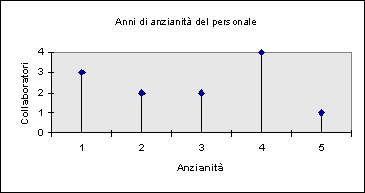
Esempio: stipendi del personale in un ufficio (caso continuo, diagramma a rettangoli).
Classi di stipendio (X) |
Collaboratori (f) |
30'000 --I 40'000 |
5 |
40'000 --I 50'000 |
6 |
50'000 --I 60'000 |
15 |
60'000 --I 70'000 |
20 |
70000 --I 80'000 |
12 |
80'000 --I 90'000 |
2 |
60 |
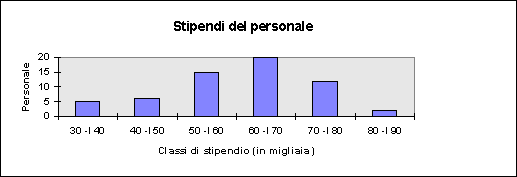
Se definissimo una nuova classe che comprendesse e sostituisse le precedenti prime due (quindi, 30'000 --I 50'000, il che avrebbe anche senso giacché, insieme, hanno una frequenza che si avvicina a quella delle classi successive), non saremmo più in grado, con l'Excel, di produrre il grafico a rettangoli, perché l'informazione relativa alla prima colonna è scorretta in quanto l'ampiezza dell'intervallo è diversa da quella delle altre barre e ciò nel grafico non risulta.
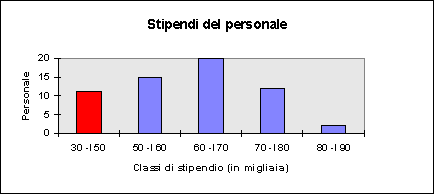
Né possiamo fabbricare da noi il grafico tenendo conto di quest'ultima osservazione,
poiché commetteremmo un grave errore !
Infatti, le aree dei rettangoli sono proporzionali alle frequenze (questo per la costanza dell'ampiezza).
Allo stesso modo, perché il grafico abbia senso, l'area totale dei rettangoli deve essere uguale all'area del poligono di frequenza (quell'area cioè sottesa dalla linea spezzata che unisce tra loro i valori centrali delle classi): ciò non accade se le classi hanno ampiezza diversa.
Vediamo perché:
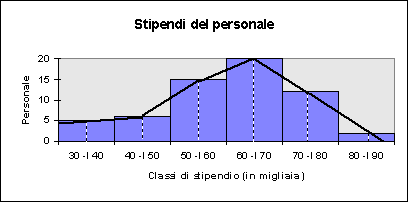
Si noterà come i "triangolini" dei rettangoli, esclusi dalla linea spezzata (cioè quella porzione di area dei rettangoli da essa non sottesi), sono compensati dai "triangolini" immediatamente successivi dello sfondo grigio.
Pertanto, il poligono di frequenza ed il diagramma a rettangoli sono equivalenti nel rappresentare graficamente la nostra seriazione ed, entrambi hanno senso.
Ma se "allarghiamo" del doppio il primo rettangolo, l'uguaglianza tra l'area totale dei rettangoli e l'area del poligono di frequenza non è più conservata:
per verificare ciò bisogna usare carta e penna perché l'Excel non permette di allargare una sola barra (appunto
perché ciò inficerebbe la bontà dell'intero diagramma).
In conclusione, per una corretta rappresentazione grafica delle seriazioni con classi di ampiezza diversa, dobbiamo utilizzare, anziché le frequenze, le densità di frequenze.
Densità di frequenza = (f / A) . 100, dove A è l'ampiezza della classe. Quindi:
Classi di stipendio (X) |
Collaboratori (f) |
Densità di frequenza (A) |
30'000 --I 50'000 |
11 |
0.05 |
50'000 --I 60'000 |
15 |
0.15 |
60'000 --I 70'000 |
20 |
0.20 |
70'000 --I 80'000 |
12 |
0.12 |
80'000 --I 90'000 |
2 |
0.02 |
60 |
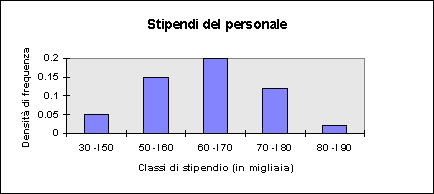
Ciò non deve sorprendere. Se non operiamo in questo modo forniamo un'informazione distorta; la stessa che forniamo quando diciamo che, ad esempio, la Svizzera è più popolata del Principato di Monaco perché, anche se è innegabile che la Svizzera ha un numero di abitanti di gran lunga superiore a quello del Principato di Monaco quest'ultimo, in realtà, fa registrare una densità abitativa (numero di abitanti/km2) di molto superiore a quello della Svizzera ed è Esso, quindi, ad essere più popolato.
Alcuni suggerimenti per ottimizzare i grafici.
1) Invertire le righe con le colonne.
È notoriamente meglio avere poche seriazioni, con pochi punti in ciascuna di esse, che avere molte serie con pochi punti.
Il grafico B è infatti preferibile al grafico A.
Esempio: personale occupato nei servizi bancari nell'arco del primo semestre dell'anno (rilevazione mensile).
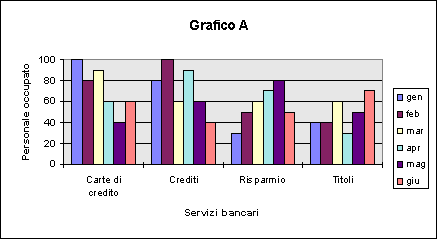
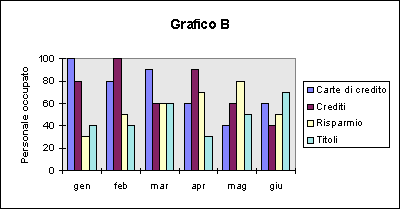
2) Tralasciare il grafico.
Per usare efficacemente i grafici, è necessario sapere quando non si deve utilizzarli !
Infatti, è molto meglio mostrare una piccola tabella di valori (con meno di 20 voci) piuttosto che un grafico. Il lettore potrà così più facilmente ricavare le informazioni veramente importanti.
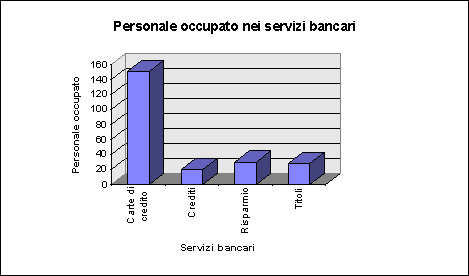
Nell'esempio che segue, la tabella è sicuramente da preferire al grafico.
Esempio: personale occupato nei servizi bancari.
Servizi bancari |
Personale occupato |
Carte di credito |
150 |
Crediti |
20 |
Risparmio |
30 |
Titoli |
28 |
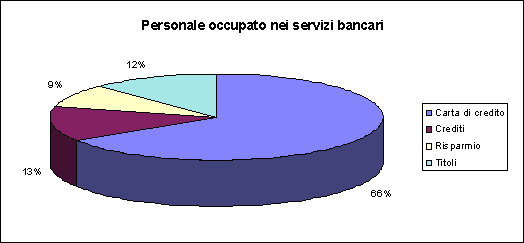
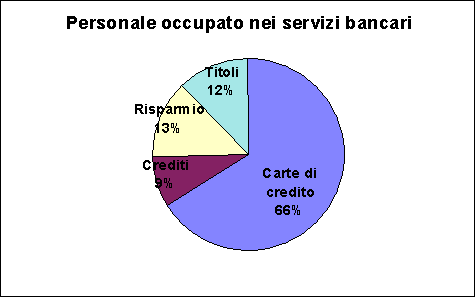
3) Far risaltare i dati.
Accertarsi che la rappresentazione abbia come protagonista sempre e solo il dato.
Minimizzare, pertanto, l'uso dei titoli, della legenda, degli assi e dei vari richiami
Il secondo grafico è da preferire al primo.
4) Mostrare anche i dati correlati.
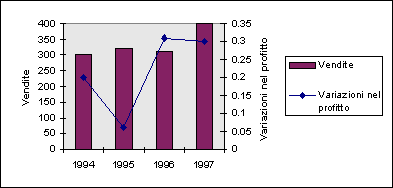
È preferibile mostrare tutti i dati che concorrono a presentare un'informazione completa.
Pertanto, i grafici combinati possono essere molto utili.
Un grafico delle vendite non è un granché utile se non considera anche l'andamento dei profitti.
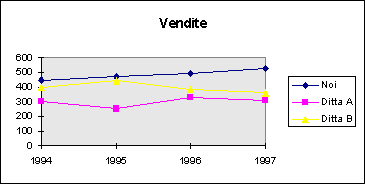
5) Comparare i dati.
L'andamento delle vendite è poco esplicativo se non lo si confronta con quello della concorrenza.
NOTE
1 Con le denominazione diagramma a rettangolo (a colonne o a righe/barre che sia), ed istogramma (istòs, in greco antico, era l'albero maestro della nave, da cui palo, barra) si intende il medesimo tipo di grafico.
2 Il diagramma a canna d'organo, disponibile in Excel come "Group Columns/Rows", permette di visualizzare contemporaneamente più seriazioni. È del tipo diagramma a rettangoli ma anziché avere, in corrispondenza di un valore di X, una sola barra ne ha tante quante sono le seriazioni considerate.
3 Se anziché operare in Excel, si sta lavorando in Word, si può creare il grafico utilizzando Microsoft Graphs che ha le stesse funzioni dei chart di Excel ma con una risoluzione un po' inferiore.
“Le decisioni d’impresa, spesso, non sono né giuste né sbagliate: noi ti aiutiamo, però, affinché esse siano sempre le migliori”.
Conseguire un vantaggio competitivo con l’analisi dei dati aziendali
Richiedete la soluzione gratuita di un vostro caso aziendale
