L'indice di miglioramento.
Ricordo che il nostro quesito é:
"Y dipende da X ? E se sì, in che misura ?"
Ciò equivale a chiederci: la variabilità osservata del fenomeno "quotazione del titolo Y" in che misura dipende (può essere spiegata) dalla quotazione del titolo B ?
In altre parole, al variare della quotazione di B, in che misura varia la quotazione di A ?
Y dipende perfettamente da X se la variabilità di Y è completamente causata dal modo con cui X varia.
Se la varianza di Y (la sommatoria degli scarti dei valori di Y dalla sua media) è uguale alla varianza di Y condizionata dalla variabilità di X (la sommatoria degli scarti delle medie di Y condizionate da X dalla media di Y), ciò vuol dire che Y dipende in media, perfettamente da X.
· Il concetto di varianza di Y condizionata da X si traduce con:
la varianza di Y spiegata da X (dovuta cioè alla dipendenza di X) adottando le medie condizionate.
· La sommatoria degli scarti tra i valori osservati di Y e quelli teorici (= medie condizionate) si traduce con:
la varianza residua (cioè quella parte di variabilità di Y non spiegata da X, quando si sono adottate le medie condizionate). È una misura del danno che si consegue dall'aver adottato le medie condizionate per descrivere la variabilità di Y.
Da notare che essa è massima nel caso si adotti, per spiegare la variabilità di Y, la sua media.
perché quest'ultima non tiene conto di X. Quindi la varianza di Y è uguale alla varianza residua.
Formalmente il legame tra i tre tipi di varianza è :
VAR(Y) = VAR(spiegata) + VAR(residua).
Verificare se Y dipende da X, significa calcolare l'indice di miglioramento (RSQ) che si ottiene nella spiegazione della variabilità di Y adottando, anzichè la media di Y, le sue medie condizionate da X. Esso è uguale al rapporto tra la varianza spiegata e la varianza di Y.
Formalmente: Im = VAR(spiegata) / VAR(Y).
Im è compreso tra 0 (perfetta indipendenza in media) e 1 (massima dipendenza in media).
Si avrà perfetta dipendenza in media se VAR(residua)= VAR(Y),=> VAR(spiegata) = 0
e perfetta indipendenza in media se VAR(spiegata)= VAR(Y) => VAR(residua)= 0.
Un po' di calcoli:
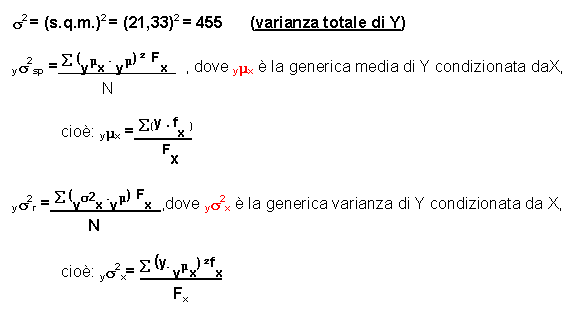
Abbiamo visto nella prima parte che le 4 medie di Y condizionate da X sono:
60, 74, 100, 70.

((60 - 73,6)2X8) + ((74 - 73,6)2X5) + (100-73,6)2X5) + (70 - 73,6)2X7) = 202,24
25
L'indice di miglioramento é, pertanto:
Im face="Garamond"= 202,24 / 455 = 0,44
La varianza residua, per curiosità, può benissimo essere calcolata per differenza:

Abbiamo così verificato che, impiegando le medie condizionate, l'andamento del titolo A (Y) è spiegato (=influenzato) per circa metà (il 44%) dall'andamento del titolo B (X).
Già, ma in che modo si influenzano i due titoli ? Che tipo di relazione è ? Lineare, esponenziale o logaritmica ? È possibile costruire un modello per effettuare delle previsioni sull'andamento del titolo A ?
Ora, quindi, vedremo come:
· misurare l'intensità e il verso di tale legame tra Y e X e come rappresentarlo graficamente;
· passare ad un grado superiore nella spiegazione della dipendenza tra X e Y.
Parleremo cioè della funzione di regressione e del coefficiente di correlazione.
“Le decisioni d’impresa, spesso, non sono né giuste né sbagliate: noi ti aiutiamo, però, affinché esse siano sempre le migliori”.
Conseguire un vantaggio competitivo con l’analisi dei dati aziendali
Richiedete la soluzione gratuita di un vostro caso aziendale
