La funzione di regressione.
Vogliamo ora rappresentare in maniera funzionale (cioè mediante una funzione analitica) la dipendenza di Y da X.
Adottando un modello lineare che riassuma la dipendenza di Y da X, è possibile associare a qualsiasi valore di X un valore corrispondente di Y senza doverci limitare ai soli dati osservati.
È così possibile regredire Y rispetto ad X: assegnando cioè arbitrariamente dei valori ad X otteniamo, mediante l'estrapolazione del comportamento osservato di Y dipendente da X, un valore teorico di Y che è il più attendibile possibile.
Possiamo, in altre parole, verificare quale é la quotazione media (=stimata) del titolo A in corrispondenza di una certa quotazione del titolo B.
Il modello lineare ha così un potere esplicativo del fenomeno maggiore di quello detenuto dalla media e dalla spezzata di regressione perché, graficamente, è rappresentato da quella linea che interpola al meglio i valori osservati, che cioè minimizza al massimo il quadrato della distanza tra valore teorico e valore osservato, consentendoci di avanzare delle previsioni su Y (regressione).
Si pongono allora due problemi:
1) la scelta del modello;
2) come misurare la capacità di adattamento del modello ai dati osservati.
1) La scelta del modello.
I moderni software statistici, anche quelli meno sofisticati, forniscono automaticamente il modello lineare che meglio si adatta ai dati.
Per esempio, la retta ,la parabola, la funzione logaritmica, quella esponenziale, ecc.
Ecco alcuni esempi:
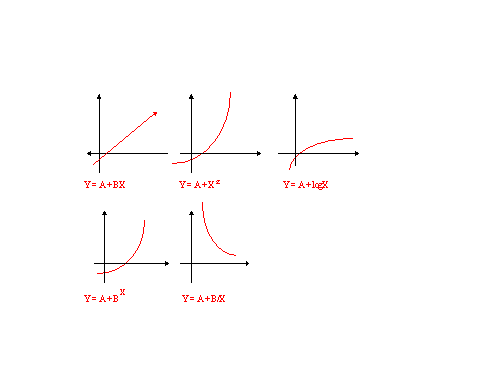
Adottiamo il modello più semplice Y = a + bX, cioè quello che esprime la retta (LINEST).
· Il coefficiente a (INTERCEPT), che sul piano cartesiano indica lo scostamento dall'origine della retta di regressione, indica il valore assunto da Y, quando X=0.
Esso non produce modificazione di Y al variare di X ed è uguale a:
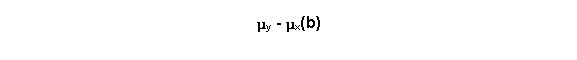
· Il coefficiente b (SLOPE), che sul piano cartesiano rappresenta l'inclinazione della retta, indica di quanto varia in media Y al variare di un'unità.
Esso indica la variazione media della variabile dipendente (Y) per una variazione unitaria della variabile indipendente (X).
È uguale a:
![]()
Dopo una semplice fattorizzazione, la funzione di regressione, nel caso della retta, assume la seguente espressione:
![]()
Le funzioni di Excel per calcolare i coefficienti sono: LINEST (nel caso della retta) e LOGEST (nel caso dell'esponenziale); quelle per regredire una variabile rispetto ad un'altra sono: TREND, FORECAST (nel caso della retta) e GROWTH (nel caso dell'esponenziale).
Purtroppo, come già detto, a causa delle loro limitazioni, esse non possono venir utilizzate per distribuzioni di frequenze.
Attenzione: la funzione LINEST, nel caso il coefficiente a sia nullo (cioè la retta passi per l'origine) fornisce dei risultati sbagliati. Pertanto, forse è meglio non utilizzarla.
Si è visto che per ricavare il coefficiente b, è necessario conoscere la covarianza.
Vediamo, allora, in che cosa essa consiste.
“Le decisioni d’impresa, spesso, non sono né giuste né sbagliate: noi ti aiutiamo, però, affinché esse siano sempre le migliori”.
Conseguire un vantaggio competitivo con l’analisi dei dati aziendali
Richiedete la soluzione gratuita di un vostro caso aziendale
